כשאתם ניצבים בפני שתי דלתות סגורות, מה הסיכוי שתפתחו את הדלת הטובה ביותר עבורכם?
X זמן קריאה משוער: 5 דקות
מרילין ווס סוואנט (Marilyn vos Savant) החזיקה בתואר האישה החכמה ביותר בעולם במשך שלוש שנים רצופות. ציון האיי־קיו שלה הרקיע לשחקים וטיפס לרמה של 228 נקודות. האמת היא שהציון ניתן לה בהיותה ילדה במבחני האיי־קיו המיועדים לילדים והוא שקול ל־185 במבחן של מבוגרים. זה לא הורס את המסיבה — הציון עדיין מופלג. אגב, אם נאמין לשמועות, לאלברט איינשטיין היתה מנת משכל של 160 נקודות "בלבד".
גברת ווס סוואנט הייתה בעלת טור בשם "Ask Marilyn" בכתב העת Parade . הטור הביא לה פרסום רב — בשיאו קראו אותו יותר מ-30 מיליון איש ואישה. במסגרת הטור מרילין פתרה חידות (לוגיות, מתמטיות , מילוליות...) והשיבה על שאלות במגוון רחב של נושאים. בספטמבר 1990 התחוללה שערורייה סביב אחת התשובות של מרילין. אלפי מכתבי תגובה הגיעו למערכת. כולם חשבו שהפעם מרילין החכמה טועה. הנה, סוף־סוף, הגאונית הוכנעה. היו קוראים שהקניטו אותה על זה שהיא אישה ולכן היא לא אמורה להתעסק במתמטיקה. אז מה בדיוק קרה באותו הטור המפורסם? ומה הייתה השאלה?
מכונית או עז
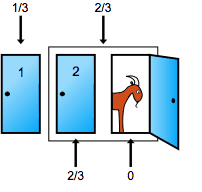
בשעשועון טלוויזיה, המשתתף עומד מול שלוש דלתות — אחת מהן מסתירה מכונית ומאחורי השתיים האחרות נמצאת עז. המנחה יודע איפה העזים ואיפה הפרס, אבל הוא לא מגלה את זה, כמובן. המשתתף בוחר דלת. כיוון שבחירתו מקרית, ברור לנו כי הסיכוי שהוא יזכה במכונית שווה לשליש. בשלב הזה, המנחה ניגש לאחת משתי הדלתות האחרות, פותח אותה וחושף עז. כרגע יש לנו שתי דלתות סגורות. אחת מהן מסתירה עז. ואז, כדי להעלות את המתח, המנחה שואל את המשתתף: "האם תרצה להחליף את הדלת שבחרת?" המשתתף מביט בדלת אחת, מביט בדלת השנייה, מתלבט, מזיע, מביט בקהל, ולבסוף באצבע רועדת הוא מורה על אחת הדלתות... וכשהדלת נפתחת הוא רואה... מכונית... או עז.
מֶהההה הבעייה? השאלה ששלחו למרילין היתה: מה כדאי למשתתף לעשות? לדבוק בבחירה המקורית או להחליף אותה? האם הסיכוי לזכייה גדל או קטן כשהמשתתף משנה את דעתו? או אולי זה בכלל לא משנה?
הבעיה של אברי גלעד
אם השאלה מוכרת לכם, זה משום שצפיתם בשעשועון הטלוויזיה "עשינו עסק" שהנחה אברי גלעד בשנות התשעים. היתה זו גרסה ישראלית לשעשועון טלוויזיה אמריקאי בעל אותו השם. השעשועון הפופולרי הוקרן בארצות הברית במשך עשרות שנים. למנחה האמריקאי קראו מונטי הול, והחידה מכונה על שמו Monty Hall Problem . אם לתרגם לעברית, אנחנו נקרא לזה הבעיה־של־אברי־גלעד. הבעיה־של־אברי־גלעד נראית פשוטה, וכמדומה כל אחד יכול להמליץ למשתתף מה כדאי לו לעשות... אז מה הייתם ממליצים? מרילין המליצה להחליף את הדלת. קוראים רבים טענו בכעס, שאין הבדל. מאחורי דלת אחת יש עז, מאחורי השנייה מכונית, זה "פיפטי־פיפטי", מי לא מבין? מה יש בכלל להבין? מרילין קיבלה קרוב ל־10,000 מכתבים (מתוכם כ-1,000 היו מבעלי תואר Ph.D) שטענו בתוקף שהיא טועה. הדבר המדהים הוא שחלק מבעלי תואר Ph.D הזועמים היו דוקטורים למתמטיקה (והם טעו). הם בזו למרילין על חוסר היכולת שלה להבין שאלה אלמנטרית בחשבון. הם כתבו למערכת מכתבים בנוסח, "כמה מתמטיקאים את צריכה כדי לשנות את דעתך?" או, "אם כל כך הרבה מדענים טועים, המדינה בצרות." והיו קוראים יצירתיים וחצופים במיוחד שכתבו לה, "את בעצמך עז."
חשוב להבין ולזכור, שהעובדה כי קיימות שתי אפשרויות בלבד אינה מחייבת שהאפשרויות האלה יהיו שוות סיכוי: או שירד מחר שלג באילת או שלא ירד, אך הסיכויים של שני המאורעות אינם שווים ולכן אינם חצי־ חצי

איור מאת ובאדיבות דני קרמן
מרילין נשארה איתנה בדעתה: כדאי להחליף את הבחירה של הדלת, כי זה מגדיל את הסיכוי לזכות במכונית. על מנת לשכנע את הקוראים הזועמים, היא קראה לעזרתם של ילדים ברחבי המדינה וביקשה מהם לערוך ניסוי. להכין 3 פתקים עם המילים "עז" "עז" ו"מכונית", ולדמות את המשחק. ילד אחד יהיה השחקן שבוחר פתק ויכול לזכות במכונית. ילד אחר יהיה המנחה שיודע מה כתוב על הפתקים וחושף פתק שכתוב עליו "עז" אחרי הבחירה הראשונה של השחקן. מרילין ביקשה מהילדים להשוות בין שתי האסטרטגיות: חזרו על הניסוי מאתיים פעם כשהשחקן מחליף את הבחירה הראשונה; חזרו על הניסוי מאתיים פעם כשהשחקן דבק בבחירה הראשונה; וְסִפְרוּ כמה פעמים זכיתם במכונית בכל אחת מהשיטות.

עטיפת הספר
מהר מאוד הגיעו מכתבים מרחבי ארצות הברית. כיתות רבות אירגנו את הניסוי במהלך שיעורי המתמטיקה. הם גילו שמרילין צודקת. מספר הזכיות גבוה יותר כשמחליפים את הדלת. האם זה עזר? לא ממש. אפילו הסימולציה כשלה בניסיונה להנחיל את התורה; אנשים פשוט סירבו להאמין ששווה להחליף את ההימור. "אם יש שתי דלתות אפשריות, לא ייתכן שהסיכויים אינם חצי־חצי" — התעקשו קוראיה של מרילין. אפילו ה"ניו יורק טיימס" פירסם מאמר ראשי שתמך בעמדתה (שהיא, כמובן, גם עמדת הכותבים של ספר זה, ומיד אחרי הסבר משכנע, זו תהיה גם העמדה שלכם) אך עדיין אנשים רבים סברו — וסבורים — שבכל פעם שיש שתי אפשרויות, הסיכויים הם חצי־ חצי. אולי זה פשוט בגנים שלנו.
חשוב להבין ולזכור, שהעובדה כי קיימות שתי אפשרויות בלבד אינה מחייבת שהאפשרויות האלה יהיו שוות סיכוי: או שירד מחר שלג באילת או שלא ירד, אך הסיכויים של שני המאורעות אינם שווים ולכן אינם חצי־ חצי; כאשר אני זורק לסל מאמצע המגרש, ישנן שתי אפשרויות בלבד — או שאקלע או שלא, ועדיין לא הייתי מהמר שהסיכוי הוא חצי־חצי — שתי האפשרויות האלה אינן שוות סיכוי; חולה נכנס לניתוח להוצאת שקדים — או שישרוד או שימות — אנו רוצים לקוות שהסיכויים אינם חצי־חצי. כך גם עם הדלתות, רק באופן גלוי פחות. שתי אפשרויות אינן מחייבות סיכויים שווים לכל אפשרות!
"אם יש סיכוי של חמישים אחוז שדבר-מה ישתבש, אזי הוא ישתבש בתשעה מקרים מתוך עשרה".
Paul Harvey שדרן ב- ABC Radio Networks
הנה הסבר מילולי: מדוע כדאי לשנות את ההחלטה?
אמנם בנקודה הזאת שהמנחה פותח דלת ומראה כי מאחוריה נמצאת עז כמעט כולם חושבים שהסיכוי של המתמודד עלה לחצי — הרי נותרו רק שתי דלתות! אבל לא. הסיכויים של המתמודד היו שליש ונשארו שליש, וזאת כי הבחירה הראשונה התבצעה מול שלוש דלתות. היתרון של הדלת האחרת טמון בכך שהיא נבחרת באופן מושכל: נדגיש, למנחה אסור לחשוף את הפרס. בנקודה הזאת, המנחה מוסיף אינפורמציה. לכן כשמציעים למשתתף להחליף את ההימור, העצה המתמטית היא — תחליף! הבעיה־של־אברי־גלעד, כמו שאנחנו קראנו לה, היא בעיה פשוטה ומשעשעת, שהפתרון שלה נוגד את האינטואיציה של רובנו. אפילו המתמטיקאי הגדול פאול ארדש (Erdős Pál) הודה שנזקק לסימולציה כדי להשתכנע שהסיכויים אינם זהים עבור שתי הדלתות . ומה אם המנחה מציע להחליף את ההימור רק לפעמים? או־אז מתעוררת השאלה — למה מציעים לי להחליף? לכך אין לי עצה, כי כאן נכנסים שיקולים פסיכולוגיים שמתערבבים עם המתמטיקה ומכשילים את החישובים הטהורים.
המאמר מבוסס על פרק מספרם של ד״ר גייל גלבוע פרידמן וד״ר חיים שפירא ״אני חושב משמע אני טועה״ שרואה אור בימים אלה בהוצאת כנרת זמורה ביתן.
 מחשבות מתחילות כאן
מחשבות מתחילות כאן

תגובות פייסבוק
28 תגובות על אני חושב משמע אני טועה
הדבר תלוי בהאם המנחה יודע איפה הפרס או לא.
אם הוא יודע כדאי להחליף - עוזר להבין זאת אם נחשוב על משחק דומה עם אלף דלתות, ששחקן בוחר אחד ואז המנחה פותח 998 דלתות ללא הפרס ואז שואל האם אתה רוצה להחליף.
אם המנחה לא יודע איפה הפרס, ובמקרה (!) מצליח לפתוח דלת ללא הפרס, אז באמת אין זה משנה אם החלפת או לא. בדוגמא עם 1,000 הדלתות הסיכוי שהמנחה במקרה יפתח 998 דלתות שבהן אין פרס הוא אפסי.
אחד ל 500 זה לא אפסי
סוף סוף הסבר שהבהיר את הסוגייה. תודה!
הסבר פשוט וגאוני! עכשיו באמת הבנתי.
תודה !
אני לא מבין. זה קשור דווקא לאם המנחה מבקש ממך להחליף? הוא לא אמור לעשות את זה כדי לנסות להכשיל אותך?
על פי חוקי המשחק המנחה תמיד חושף עז ואז מציע למשתתף את הדלת החלופית שנותרה: אם הבחירה של המשתתף השאירה למנחה מכונית ועז, אז בדלת החלופית תהיה מכונית; אם הבחירה של המשתתף השאירה למנחה שתי עזים, אז בדלת החלופית תהיה עז.
בכל מקרה, מנחם, הכוונה של המנחה (בין אם טובה ובין אם רעה) לא תשפיע על מהלך הדברים.
אחרי הדלת השלישית נותרות שתי דלתות, באחת עז ובשנייה מכונית. למה הסיכויים לזכות במכונית לא משתנים?
איך בדיוק הסיכויים נשארו שליש?
בדלת שהוא פתח הייתה עז, ועכשיו נשארו שני דלתות. אחת בלי מכונית והשנייה עם זה.
העובדה שהמשתתף בחר בדלת כשהיו שלושה אפשרויות, לא רלוונטית כלל..ישנם שתי אפשרויות, פיפטי פיפטי.
האמת היא שדווקא הציור הוא זה שגרם לבחורה של 3 יחידות לפתור את החידה ולא ההסבר המילולי. אבל הנה התשובה. נחלק את סיכויי הזכייה בפעם הראשונה שווה בשווה כך הסיכוי הוא שלישי בכל דלת. אם לא נחשיב כרגע את הדלת שבחרנו, הסיכוי שבאחת מהדלתות שלא בחרנו תהייה המכונית הוא 2/3. כעת מראים לנו שבאחת משתי הדלתות הללו יש עז. לכן בתחילה החישוב שלנו היה ששתי דלתות שוות 2/3 ועוד הדלת שבחרנו שווה 1/3 אך מכיוון שאנחנו יודעים שבאחת משתי הדלתות יש עז, הסיכוי של הדלת השנייה שלא בחרנו גדל ל-2/3 ולכן כדאי להחליפה
שרון, שלומי, ברגע קבלת ההחלטה המשתתף עמד מול שלוש דלתות. לכל אחת מהן הסתברות זהה להסתיר את הפרס: כלומר 1/3.
העזים... המכונית... הכל נשאר במקום גם אחרי פעולות המנחה, ולכן נשארת אותה התשובה לשאלה הבאה: האם יש פרס מאחורי הדלת שנבחרה על ידי המשתתף?
העובדה שזה לא אינטואיטיבי יוצרת את העניין סביב השאלה.
אבל אפשר להגיד דבר דומה על הסיכוי שתהיה מכונית אחרי הדלת שלא נפתחה והמשתתף לא בחר בה. בהתחלה היה שליש, ולאחר הפתיחה היה שליש, כי שום דבר לא השתנה. אז שליש לדלת שלא נבחרה, ושליש לדלת שנבחרה. סיכוי שווה.
ואם נניח שיש שני משתפפים בו זמנית שכל אחד בחר דלת.
אחד עז והשני מכונית.
והמנחה פותח דלת שלישית שיש בה עז.
ומציע לכל אחד מהם להחליף דלת.
במקרה הזה לבוחר בדלת מכונית לא כדאי להחליף ולשני כן.
אך אף אף אחד לא יודע מה יש אחרי הדלת שלו לכן ההשארות בבחירה הראשונה או החלפה שווים חמישים חמישים.
במקרה שלך זה 50 50 כי למנחה אין בעצם ברירה, הוא תמיד בוחר בדלת השלישית, (גם אם יש בה מכונית) ולכן פתיחת הדלת לא תרמה אינפורמציה. לעומת המקרה הרגיל בו המנחה לעולם לא פותח את הדלת עם המכונית, פתיחת הדלת ע"י המנחה תרמה אינפורמציה.
אהבתי שהכותרת של החלק האחרון היא ״הנה הסבר מילולי: מדוע כדאי לשנות את ההחלטה?״ ואין בה הסבר מילולי למה כדאי. בתגובות יש כמה הסברים, השלם ביותר הוא של מעיין בתגובה לשלומי.
לא הבנתי למה זה חשוב שהמנחה יודע איפה המכונית. נניח שאיננו יודע. בחרתי את דלת א', המנחה שאיננו יודע פותח את דלת ב', והנה מאחוריה מכונית. גמרנו, המשחק נגמר. הוא איננו שואל אותי שאלות ואני הולך עצוב הביתה.
פתח את דלת ב', והנה עז. ואז הוא שואל אותי האם אעדיף להישאר בבחירה המקורית.
אחזור להתחלה. נניח שהמנחה שואל אותי מה הבחירה שלי: דלת א', או שתי הדלתות ב' וג'? ברור. עדיף לבחור ב' וג'. המנחה אומר: OK. פותח את ב', והנה עז, ושואל: אתה נשאר בבחירה או מחליף? אני נשאר. הרי הסיכוי שהמכונית מאחורי ב' או ג' הוא 2/3. לא? (ובסוד, היא לא מאחורי ב'!).
הרעיון של עודד לגבי 500 דלתות מחזק כמובן את החישוב. שואלים את המתמודד: מה אתה מעדיף: דלת אחת (ומהי הדלת שאתה בוחר), או את 499 הדלתות האחרות? צריך להיות אידיוט לבחור דלת אחת, ולא את כל יתר הדלתות. לאחר שהמנחה פתח 498 מתוך 499 הדלתות "האחרות", לאיזו דלת יש יותר סיכוי?
אם המנחה אכן יודע איפה המכונית, הוא יפתח בביטחון דלת אחר דלת, עד שיישארו שתי דלתות סגורות. אם איננו יודע, קרוב לוודאי שבאחת הדלתות שהוא פותח תימצא המכונית. אבל אז ממילא המשחק נגמר ולא מגיע הרגע שבו נשאלת השאלה "האם אתה מבקש להחליף את בחירתך". לכן, נדמה לי שלא חשוב אם המנה יודע איפה המכונית.
המוקש האמיתי בכל "דילמת אברי גלעד" הוא לדעתי (ולדעת גדולים ממני, אשר אפילו ההבנה הזאת הביאה להם פרס נובל) המוקש הפסיכולוגי. מה יהיה אם בסופו של דבר יסתבר שהמכונית נמצאת מאחורי הדלת שבה בחרתי בהתחלה? זה הרי יהיה אסון! אני אתאבד! ואכן, שמעתי מכמה אנשים שזאת הסיבה שלא היו מחליפים.
כל התרגיל נראה אחרת אם אומרים למתמודד בהתחלה להצביע על אחת הדלתות (לא אומרים לו "לבחור"), ואז פותחים אחת הדלתות האחרות, ורק אז אומרים לו "לבחור": את הדלת שעליה הצביע בהתחלה, או את הנותרת מהשתיים האחרות. המתמודד לא יצר "הזדהות" עם הדלת שעליה הצביע.
הכי פשוט זה לשאול אותו בהתחלה האם הוא רוצה לבחור שתי דלתות או דלת אחת.
למרות השימוש בצורת שאלה שונה, מבחינת ההסתברות שלושת הצורות הן זהות.
(זאת דוגמא אחת מיני רבות שבה הבגד עושה את האדם)
בודאי שזה משנה אם המנחה יודע או לא. במקרה שהוא יודע אז מכיוון שרק בשליש מהמקרים אני בוחר בהתחלה בדלת הנכונה בהכרח שבשני שליש מהמקרים אם אחליף אני אזכה. לעומת זאת אם המנחה מנחש אז בשליש מהמקרים אני מנחש בדלת הנכונה, בשליש השני אני טועה והמנחה פותח פרס, ובשליש השלישי שנינו טועים. כעת אם אני מגלה שהשליש השני לא נכון נותרו לי שני אירועים שההסתברות שלהם שווה. אני צודק או ששנינו טועים. כלומר 50 50.
"היתרון של הדלת האחרת טמון בכך שהיא נבחרת באופן מושכל: נדגיש, למנחה אסור לחשוף את הפרס. בנקודה הזאת, המנחה מוסיף אינפורמציה..."
נדמה שאולי פוספס פה משהו - גם אם לא ידוע אם המנחה בוחר באופן מושכל או לא (אבל ידוע שהוא עושה זאת תמיד), כדאי להחליף. זאת מכיוון שאם הוא עושה זאת באופן מושכל אז ברור שכדאי להחליף ואם לא - אז זה 50 50, לכן אם נחליף לא נפסיד. כלומר ההחלפה היא אסטרטגיה עדיפה או שווה ולכן ברור שכדאי לבחור בה.
הסיכוי הוא 50 50 ביחס לשתי הדלתות ושליש ביחס לשלושת הדלתות
הבעיה היא במוח של מתמטיקאים שמתייחס לדברים רק ברמה מסויימת ולא עוצרים לחשוב אם יש אי הבנה
לכל צי שעדייו לא סגור על הסיבה שזה 2/3 ולא 0.5:
חישבו על התרחיש המורחב הבא: 1000 דלתות. באחת יש מכונית ובשאר יש עזים. בחרתם דלת. לפני פתיחתה המנחה חושף 998 דלתות שבהן עזים. שוב אתם נשארים מול 2 דלתות סגורות אשר באחת מכונית ובאחת עז. האם הסיכויים הם 50-50? בוודאי שלא. אם תשארו בדלת המקורית הסיכוי לזכייה הוא 1/1000. אם תחליפו דלת הסיכוי לזכייה הוא 999/1000.
פתיחת הדלתות עם העיזים חשפה מידע חשוב. היא צמצמה את אי הוודאות לגבי מיקומה של הדלת עם הפרס מ-1000 אפשרויות ל 2 אפשרויות. הסיכוי שמראש בחרת את הדלת הנכונה היה ונשאר 1/1000 ולכן הסיכוי שהדלת השניה שנותרה תסתיר מאחוריה את הרכב הוא 999/1000.
אפשר להיתווכח על הפרשנות, על ההיגיון של הפיתרון הנכון (שהוא שעדיף להחליף את הבחירה), אבל מוזר שיש המתווכחים מהו הפתרון הנכון. הרי אפשר בקלות לבדוק מה קורה במציאות, לנסות שוב ושוב, וזהו.
לדעתי, הפרט הכי חשוב במאמר הוא שאכן נעשה ניסוי, נקבעו ההסתברויות האמיתיות, עדיין היו כאלה שטענו שהסיכויים אחרי פתיחת דלת אחת הם חצי חצי בין שתי הדלתות הנותרות.
ולמרות זאת, עדיין נשאר "אני מאמין ש..." או: "כמה מתמטיקאים את צריכה כדי לשנות את דעתך?"
מה גדול התסכול כאשר אתה רואה את מה שנכון, אבל כל האחרים "חושבים", (אבל בעצם מאמינים!) אחרת.
לפני הרבה שנים היה בעיתון הילדים "הארץ שלנו" סיפור מצויר בהמשכים, אפרים חד עין. הסיפור היה על ילד שיש לו "ראיה רנטגנית", היה רואה דברים שאחרים אינם רואים. הוריו לוקחים אותו לרופא, שמאשר שאכן יש לו ראיה שחודרת מבעד למסכים. הרופא אומר להורים לצוות על ילדם שלא ידבר על הדברים הניסתרים שהוא רואה, "פן יבולע לו". בפרקים הבאים מסופר על כל מיני התרחשויות שנגמרות במשפט הקבוע: "ואני צריך לשתוק!"
וזה, כילד, קומם אותי.
אך נביאי האמת, בהבדל מנביאי השקר, לא נשמעו לציווי לשתוק, יהיה המחיר אשר יהיה.
והציווי הזה, הנון קונפורמיסטי, שלא לשתוק, בזכותו אנחנו מה שאנחנו.
וזה נכון כמובן גם באשר לכל שטחי החיים.
(הערת אגב, בהזדמנות אחרת תגיע התייחסות לילד בבגדי המלך החדשים, אבל שם המקרה שונה ממקרה אפרים חד עין)
רק שהבדיקה האמפירית היא לעולם סטטיסטית בלבד ולכן לא יכולה לבדה להוכיח משהו באופן ודאי (כמו את ההסתברות באינסוף בדיקות)
ההסבר, גם אם נכון, נכון רק במידה ומתמטיקה היא הפתרון לכל בעיה.
מאחר וישנם נעלמים בעולם כמו גם במתמטיקה, הרי שמן הסתם לא ניתן לספק תשובה חד משמעית. בטח לא נחרצת. גם אם לכאורה הוכחה בעזרת ניסוי.
תוצאות הניסוי, לא פעם, מושפעות מהלך הרוח של עורכיו.
אנשי ההגיון, הסבורים ( או יש לאמר משוכנעים) שיש לכל בעיה פתרון, יסכימו עם תוצאות המחקר.
אנשי הרגש ידבקו באינטואיציה שלהם כך או כך.
והמנצחים הם אלו היודעים לאזן בין זה לזה, מתוך הידיעה הבסיסית שלהם כי נעלם הוא נעלם הוא נעלם.
מ.ש.ל היו- 2 עזים ומכונית (;
תגובה לצהלה כהן:
מתמטיקה אינה הפתרון לכל בעיה אבל מכיוון שבמקרה הנוכחי כן מדובר על בעיה מתמטית, אז דווקא כן אפשר לדבר על תשובה נחרצת. נחרצת במובן זה שתגדיל את הסיכויים לזכות.
אין זה אומר שאדם שנמצא בסיטואציה הנ"ל חייב לשנות את בחירתו המקורית. המתמטיקה בסה"כ מראה שכדאי לו לעשות כך.
תגובה לצהלה כהן:
מתמטיקה אינה הפתרון לכל בעיה אבל מכיוון שבמקרה הנוכחי כן מדובר על בעיה מתמטית, אז דווקא כן אפשר לדבר על תשובה נחרצת. נחרצת במובן זה שתגדיל את הסיכויים לזכות.
אין זה אומר שאדם שנמצא בסיטואציה הנ"ל חייב לשנות את בחירתו המקורית. המתמטיקה בסה"כ מראה שכדאי לו לעשות כך.
למי שלא הבין, להלן שלושת הבחירות והתוצאות:
1.בחרתי דלת עם מכונית, המנחה פותח דלת עם עז ״א״ או ״ב״ (נשארה דלת עם עז)
2. בחרתי דלת עם עז ״א״, המנחה פותח דלת עם עז ״ב״ (נשארה דלת עם מכונית)
3. בחרתי דלת עם עז ״ב״, המנחה פותח דלת עם עז ״א״ (נשארה דלת עם מכונית)
הסבר מנצח! תודה
1. זה מדהים, עד כמה הבעיה הזאת, שאיננה חדשה, וכבר נכתבו עליה אינספור מלים, ממשיכה להטריד כאילו כרגע נוסחה.
2. התשובה האולטימטיבית לשאלה נמצאת בניסוי שבו עשו סימולציה הרבה פעמים, והתוצאה שכדאי להחליף. אז מעבר לזה הויכוח "מה נכון לעשות" ניגמר. נשאר הויכוח מהי נוסחת החישוב המתאימה לתוצאה הידועה.
3. לגבי התחשיב של קראוזה: הוא מבחין בין העיזים. (וזה יפה, מי שמכיר עיזים טוען שכל עז היא עז בדרכה שלה). אבל אז יש ארבע אפשרויות: 1. בחרתי דלת עם מכונית, המנחה פותח דלת עם עז א', 2. בחרתי דלת עם מכונית, המנחה פותח דלת עם עז ב'. 3. בחרתי דלת עם עז א', 4. בחרתי דלת עם עז ב'. בשתי אפשרויות המכונית מאחורי הבחירה המקורית, בשתי אפשרויות מאחורי הדלת האחרת. אז כנראה זה לא נכון. תרועת הניצחון איננה מוצדקת. (אבל ככה זה בחיים).
אתה מכניס פרט חסר משמעות
1 זו בחירה אחת ( שלי ), בחרתי דלת עם מכונית, המנחה פותח דלת עם עז ונשארת דלת עם עז
שתי הבחירות הנוספות, בחרתי דלת עם עז והמנחה פותח דלת עם עז, נשארת מכונית 2/3 סיכוי למכונית עם החלפת הדלת לאחר שהמנחה פותח דלת עם עז
הילד עם חצי המוח
מייקל רובינובעל ואישה מוצאים את עצמם בעמדה בלתי אפשרית: כדי להציל את בנם...
X 21 דקות
כוכבים
יש כוכבים לבנים, כחולים, ירוקים, אדומים.
יש כוכבים-דגים, כוכבים-פסנתרים, כוכבים-ילדוֹת,
כוכבים-מעופפים, כוכבים-פרחים, כוכבים-קיכלים,
יש כוכבים שרואים, ששומעים,
אחרים הם חרשים ואחרים עיוורים.
יש הרבה יותר כוכבים מאשר מכונות, בורגנים ופועלים:
יש כמעט רק כוכבים.
מורילו מנדס (Murilo Mendes), היה משורר ברזילאי, מודרניסט וממובילי הסוריאליזם בשירה הברזילאית, שנולד ב-1901 והלך לעולמו ב-1975. מורילו מנדס לימד ספרות ברזילאית באוניברסיטאות רומא ופיזה.
תרגם מפרוטוגזית: יורם מלצר
נעמה לי אהבתך
ריינה כהןואולי במרכז החיים מוטב להציב את חברות הנפש, ולא את מסגרת הנישואין? |...
X 23 דקות